如果给全世界学生最讨厌的学科排个名，我相信数学八成会勇夺第一（中国唯一能够撼动数学课这个地位的，估计只有政治课）。虽然很多人讨厌这门课，却也都不否认数学的重要性，无论曾经是学霸还是学渣，一旦变身为家长，立刻就会极尽手段逼迫孩子学好数学。

但是，当我们希望孩子学好数学的时候，我们真的是希望他“数学”好，还是希望他“数学考试成绩”好？当我们谈论数学时，我们究竟在谈什么？

学数学，究竟有什么用？

我不想说什么“无用之用，方为大用”这种听了会打瞌睡的话（实际上除了“数论”研究的少数领域之外，那些我们曾经以为很无用的数学发现，比如圆锥曲线、群论、非欧几何……都已经在各个对现代文明至关重要的领域里成了核心基础）。

数学的力量，首先在于把复杂问题简单化，那些简单的模型，可以帮助我们解决极端复杂的问题。

举个例子，二进制，这个世界上最简单的计数方式，只有0和1两个数字符号。除了计数之外，这两个数字还能表示逻辑中的“是”与“非”。十九世纪英国的一位中学数学老师布尔，就根据二进制的第二个特征，发明了用数学运算解决逻辑问题的方法，这个方法，现在被称为布尔代数。

乔治·布尔（George Boole，1815~1864）

布尔代数非常简单，几句话就可以说明白。整个运算的元素只有两个：1（代表是），0（代表非）。全部运算也只有与（AND）、或（OR）、非（NOT）三种。

比 如

在AND运算中，“大肚皮老师是男的”这个判断为“是”（1），“大肚皮老师有四条腿”这个判断为“非”（0），那么，“大肚皮老师是男的并且有四条腿”这个判断就为“非”（0）。

在OR的运算中，“大肚皮老师比赛得了第一名”的判断为“非”（0），“小叶老师比赛得了第一名”的判断为“是”（1），那么，“大肚皮老师或者小叶老师得了比赛的第一名”的判断就为“是”（1）。

NOT运算就更简单了，“大肚皮老师是男的”这句判断为“是”（1），那么，“大肚皮老师不是男的”这句判断就为“非”（0）。

这些就是布尔代数的全部内容，是不是超级简单？这么简单的东西，能用来做什么？

克劳德·艾尔伍德·香农（Claude Elwood Shannon，1916-2001）

1938年，香农博士提出了用布尔代数来实现开关电路的想法，所有的数学和逻辑运算，加减乘除开方乘方等等，全都能转换成二值的布尔运算。正是依靠这一点，以布尔代数作为数字电路的基础，人类用一个个开关电路最终搭出了世界上第一台电子计算机。

《模仿游戏》

从《模仿游戏》电影里那个咔咔作响的巨型机器，到今天每个家庭桌子上的笔记本、台式机，以及我们看到的电脑页面、搜索引擎，不论在工程上如何复杂，原理上依然简单，即等价于布尔运算。

就是这样一个简简单单的运算方式，甚至一直到布尔去世，都没人认为他是一个数学家，却带给了我们一个看待世界的全新视角，开创了今天的数字化世界。

这就是数学的力量，或者说，这就是数学思维的力量。

再举一个略显复杂的例子：概率论。在十九世纪之前，概率论一直局限于对静态的随机变量的研究，但十九世纪之后，发展到了对随机变量的时间序列的研究。也就是从随机变量的研究发展到了对随机过程的研究，这个发展在哲学意义上被认为是人类认知的一次飞跃。但是，随机过程的计算要复杂得多。

比如我们要研究一个城市里每天的最多人口数的话，这里面每个状态都是随机的，而且任意状态都可能和周围其他的状态相关，比如任何一天的最多人口数，与这段时间之前的最多人口数是相关的。

这样随机过程就有了两个维度的不确定性，数学家为了解决这个问题，提出了一种简化的假设，即随机过程中的各个状态，只与前一个状态有关。比如对一个城市的最多人口的研究，硬性规定今天的最多人口数只与昨天有关，而与前天无关。

虽然这种假设未必适合所有的应用，但是至少对以前不好解决的问题给了近似解，这个假设后来被命名为马尔可夫假设，而符合这个假设的随机过程，被称为马尔可夫链。

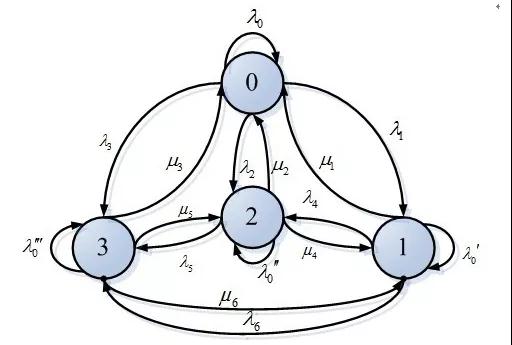
马尔可夫链

20世纪80年代末期，李开复采用隐含马尔科夫模型的框架，成功研发出了世界上第一个大词汇连续语音识别系统Sphinx。最近二十年，隐含马尔科夫模型陆续成功应用于机器翻译、拼写纠错、图像处理、基因序列分析等等多个领域，直到今天，马尔可夫模型还广泛应用于股票预测和投资。

牛顿说：真理在形式上从来都是简单的，而不是复杂和含混的。

也许有人会认为，数学问题只在理工方向有用，而对于希望往文科领域发展的人意义不大。那我们看另外一个例子，关乎历史的，我们先看一组数据：

• 中国第一个大一统王朝，秦朝建立的时候，人口数大约是4500万，十四年之后秦朝灭亡，楚汉战争，到汉初的时候人口不足2000万。

• 接下来是文景之治，人口开始缓慢恢复，到了汉武帝，人口又到了4000万，汉武帝穷兵黩武，导致全国人口减半，最低的时候又到回了2000万的规模。

• 然后是昭宣中兴，到了汉平帝，人口超过了五千万，结果王莽篡位西汉灭亡，诸侯纷争，到了东汉初年，人口又回到了2000万，然后又是光武中兴，人口再度缓慢恢复。

即便我们没有看过马尔萨斯的《人口论》，也会发现历史好像有个人口的天花板，超过这个天花板就会爆发饥荒、战争，导致人口锐减，接下来又是缓慢的盛世中兴，开始另一个循环周期。

《人口论》马尔萨斯

如果把时间尺度扩大到整个人类历史，就会发现同样的循环周期在过去几千年里重复上演。（粗略来说，就是人口的增长受土地等生活资料的限制，食物的供给达不到人口数量的增长速度，就必然导致灾难。但要注意，工业革命之后，这种循环就被打破了，中国近现代的一些大饥荒、人口锐减，纯粹是执政者的倒行逆施造成的。）

现在越来越多的学者开始从数学角度，来发掘人类历史中的现象和规律，这门新科学被称为计量历史学。

所以有历史学家认为，人类历史上实际只发生了一件事情，那就是工业革命。

我们看到，数学不仅仅只能应用在理工领域，这种高度抽象的能力、用简单模型处理复杂事物的方式，会给我们的世界打开一扇新的大门。

许晨阳博士说：这个世界很大，人类想要掌握它的规律的话，需要一定的语言，需要一定的描述方式。数学某种程度上是描述世界的一种基本语言。并不是我们创造了它，而是它一直在那里，我们发现了它而已。它是一种艺术，一种结构很美的东西。

如果你希望孩子领略一下数学世界的奇妙和美好，那么，大肚皮老师的数学课，会是一个不错的选择。

（本文转自埃尔特订阅号，作者张释文）